4. Körmozgás

Most leginkább az egyenletes körmozgást fogjuk megvizsgálni. Egyenletesnek nevezzük azt a körmozgást, aminek pályája kör, és a test által befutott ív egyenesen arányos a befutás idejével.

Számtalan példa akad az életben erre is, leírnál néhányat? Földi viszonylatban könnyen találunk ilyet?

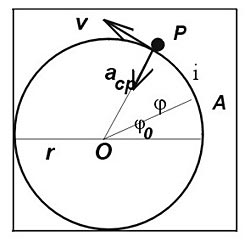
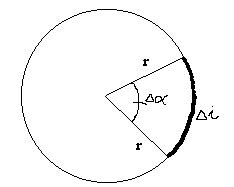
Az egyenletes körmozgás kinematikája:

Olyan állandó sugarú körpályán történő mozgás, amelynek során a test egyenlő idők () alatt egyenlő szögeket () fordul el, a mozgás bármely szakaszán. Emiatt a hányados állandó, neve szögsebesség (). A szögelfordulás ahol a kezdeti szögelfordulás. (A szögelfordulást mindig radiánban mérjük.) Egyenletes körmozgást végző test gyorsulása mindig a kör közepe felé mutató (centripetális), nagysága , ahol a kerületi sebesség, itt az ívhosszt jelöli. Egy körülfordulás ideje a periódusidő (T), mértékegysége az s (secundum). Az egységnyi idő alatti fordulatok száma a fordulatszám (jele: n ) mértékegysége az (egy per secundum).

Az egyenletes körmozgás dinamikája:

Képzeljünki el egy teherautót, amely egyenes vonalú egyenletes mozgással halad előre, jeges platóján jó nagy ládával. Egy pillanatban letérítjük autónkat útjáról, és erőnek erejével körpályára állítjuk, egy kanyart próbál sofőrünk bevenni.Ekkor tehát irányának megváltoztatásához volt szükségünk erőre, szemben a korábbiakkal, amikor sebességének megváltoztatásához kellett. Gondolatban kössük ki a ládát egy kötéllel! Ha a kötél állása a teherautó által leírt kör közepe felé mutat, akkor marad egyensúlyban a platóhoz képest a láda. A ládát körpályára kényszerítő erő tehát a körpálya közepe felé mutat. A ládát körpályán tartó erőt centripetális erőnek (jele: ) nevezzük. Ez arányos a tömegpont tömegével (m), a tömegpont sebességének (v) négyzetével és fordítottan arányos a körpálya sugarával (r). Így kiszámolási módja: A centripetális erő állása sugár állású, mindig a körpálya közepe felé mutat.

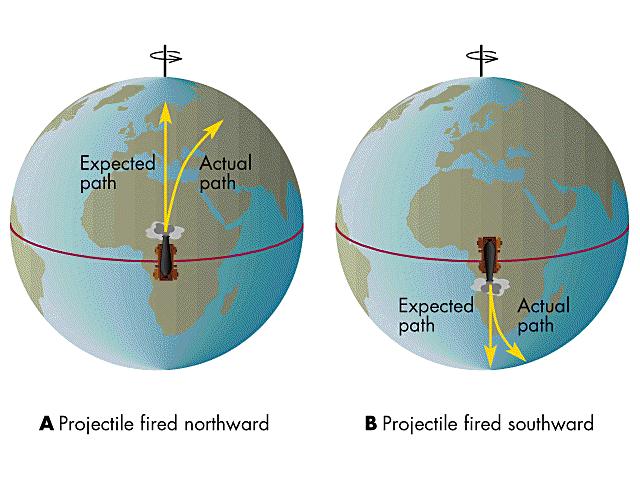
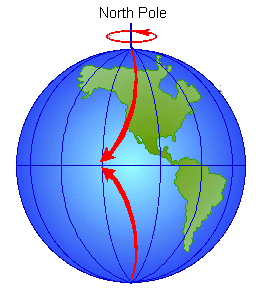
Kis emlékeztető a Föld tengely körüli forgásáról:
A MOZGÁS JELLEMZŐI:

A forgás időtartama: A Föld képzelt tengelye körül, melynek felszíni döféspontjai a földrajzi pólusok kb. 24 óránként (23 óra 56 perc 4 mp) tesz meg egy teljes fordulatot. Ez az időtartam a csillagnap.

A forgás iránya: az északi sarkpont felől nézve az óramutató járásával ellentétes, tehát nyugatról keletre tart, ezt a csillagászatban direkt forgásiránynak nevezzük.

A forgás sebességét a szögsebességgel és a kerületi sebességgel jellemezhetjük. A szögsebesség a földfelszín minden pontján egyforma (15°/óra), a kerületi sebesség azonban a forgástengelytől való távolsággal nő, így az Egyenlítőn 461 m/s, a pólusokon pedig 0 m/s.

Miért döntik meg kanyarban az úttestet, sínpályákat? Miért izmos a Forma 1 pilótáinak a nyaka?
A hidakat domborúra építik, nem homorúra. A statikai megfontolásokon kívül még miért?
Ha egy függőhíd teherbírásában nem vagyunk biztosak gyorsan szaladjunk át rajta, hogy rövidebb ideig legyünk életveszélyben, vagy lassan? Miért?

A forgásról eszünkbe juthat bolygónk mozgása is. Tavaly megismertük a Coriolis-erőnek nevezett erőtt, amely a sarkok felől vagy sarkok felé mozgó légtömegeket, repülőket, stb. téríti ki látszólag, ha a felszínhez próbáljuk viszonyítani mozgásukat.

Mekkora a kis és nagymutató végpontjának a keringési ideje, fordulatszáma és szögsebessége? Mekkora a szögelfordulásuk negyed óra alatt?

Mekkora erőt fejt ki a 100 m/s sebességgel függőleges síkú, 800 m sugarú körpályán haladó pilótára az ülés a pálya legfelső, ill. legalsó pontján?